Додаток 5

Приклади розв’язування географічних задач

1. Масштаб. Визначення відстаней на плані та карті. Якщо вам необхідно перевести един вид масштабу в інший, згадайте, ще масштаб показує, скільки сантиметрів на місцевості міститься в одному сантиметрі на карті. Тобто в числовому масштабі як чисельник, так і знаменник виражені в сантиметрах. Наприклад, масштаб 1: 1000 означає, що в 1 см на карті міститься 1000 см на місцевості, або 10 м. Інший приклад: перевести числовий масштаб 1 : 50000 в іменований. Запис іменованого масштабу буде виглядати так: в 1 см - 500 м.

Розв’яжемо задачу: визначте відстань на місцевості між двома містами, якщо відстань на карті, виміряна лінійкою, становить 3 см, а масштаб карти 1 : 2 000 000.

Розв’язок. Спочатку переводимо числовий масштаб в іменований: 1: 2 000 000 = в 1 см - 20000 м, або в 1 см - 20 км. Тепер масштаб карти слід помножити на відстань у сантиметрах, виміряну лінійкою на карті: 20 км х 3 см = 60 км.

2. Азимут. Для визначення азимутів слід пам’ятати, що це кут між напрямком на північ і якийсь об’єкт на місцевості чи плані, тому його вимірюють у градусах. Корисно скористатися такими даними: азимут на об’єкт, що знаходиться точно на сході, дорівнює 90°, точно на півдні - 180°, точно на заході - 270°, на півночі - 0°. Обчислювати азимут завжди потрібно рухаючись від півночі за годинниковою стрілкою.

Розв’яжемо задачу. Визначте, у якому напрямку повертатимуться учні з екскурсії до парку, якщо їхня школа знаходиться на північному сході, а парк - з протилежного від школи боку. Який азимут мають школа і парк?

Розв’язок. Для розв’язання задачі спочатку потрібно з’ясувати, яка сторона горизонту буде протилежною щодо школи (можна скористатися кресленням).

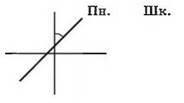
З креслення видно, що сторона, протилежна до школи, південно-західна. Отже, парк розташований на південному заході. Азимут школи (А1), що відповідає північно-східному напрямку, становить 45°. Азимут парку відповідно А2 = 225°. Робимо висновок: учні будуть повертатися з парку в північно-східному напрямку.

3. Температура повітря. Для визначення температури повітря між двома пунктами, що розміщені на різній висоті, слід пам’ятати, що температура з висотою закономірно знижується приблизно на 0,6 °С на кожні 100 м висоти. Коли повітря опускається, його температура підвищується на кожні 100 м на 1 °С (опускається повітря завжди сухим).

Розв’яжемо задачу.

А) Визначте, якою буде абсолютна висота гори, якщо температура повітря біля її підніжжя, що розташоване на висоті 250 м від рівня моря, становить + 26 °С, а на вершині +2 °С.

Розв’язок. Щоб знайти абсолютну висоту гори (h), потрібно до висоти, на якій розташоване підніжжя гори (h1), додати висоту самої гори від підніжжя до вершини h2: h = h1 + h2. Показник h1 нам відомий з умови задачі - 250 м. Щоб знайти h2, потрібно визначити, на скільки градусів знизилася температура повітря між підніжжям і вершиною гори: +26 °С - (+2 °С) = на 24 °С.

Далі складаємо пропорцію, щоб визначити висоту гори від підніжжя до її вершини:

0,6 °С - 100 м

24 °С - X м

Отже: 24 х 100 : 0,6 = 4000 м. h2 = 4000 м.

Тепер визначаємо абсолютну висоту гори: 250 м + 4000 м + 4250 м. Відповідь: h = 4250 м.

Б) Насичене вологою повітря, піднімаючись схилом гірського хребта, поступово охолоджується. Визначте температуру повітря на вершині хребта, якщо біля підніжжя температура становила +10 °С, а його висота - 2500 м. Якою буде температура повітря біля підніжжя на протилежному схилі хребта?

Розв’язок. Спочатку розрахуємо, на скільки градусів зміниться температура повітря, яке піднімається вгору. Для цього складемо пропорцію:

0,6 °С - 100 м

X °С - 2500 м

Отже, 0,6 °С х 2500 м : 100 м = 15 °С. Тепер обчислимо, якою буде температура повітря на вершині хребта: для цього від температури повітря біля підніжжя +10 °С віднімемо 15 °С: + 10 °С - 15 °С = -5 °С. Температура на вершині хребта дорівнює -5 °С. Знаючи, що при опусканні повітря його температура підвищується на кожні 100 м на 1 °С, визначимо, на скільки градусів підвищиться температура повітря при його опусканні. Складаємо пропорцію:

1 °С - 100 м

X °С - 2500 м, отже: 1 °С х 2500 м : 100 = 25 °С.

Тепер можемо обчислити, якою буде температура біля підніжжя на протилежному схилі хребта: -5 °С + (+25 °С) = +20 °С.

Відповідь: Температура повітря біля підніжжя на протилежному схилі хребта становитиме +20 °С.

4. Атмосферний тиск. Для визначення атмосферного тиску з висотою слід пам’ятати, що в нижніх шарах тропосфери з підняттям угору на кожні 12 м атмосферний тиск знижується в середньому на 1 мм рт. ст., або 1,33 гПа.

Розв’яжемо задачу. Обчисліть у гПа атмосферний тиск на вершині г. Говерла (2061 м), якщо біля підніжжя він дорівнює 766 мм рт. ст.

Розв’язок. Насамперед визначимо, на скільки мм рт. ст. зміниться атмосферний тиск при піднятті на вершину. Складаємо пропорцію:

1 мм рт. ст. - 12 м

X мм рт. ст. - 2061 м

Отже: 1 мм рт. ст. X 2061 м : 12 м = 172 мм рт. ст.

Далі визначаємо, яким стане тиск на вершині: 766 мм рт. ст. - 172 мм рт. ст. = 594 мм рт. ст. Тепер переводимо тиск в мм. рт. ст. на тиск в гПа: 1,33 гПа х 594 мм рт. ст. = 790 гПа.

5. Вологість повітря. Для визначення абсолютної (g) чи відносної (r) вологості повітря слід використовувати таку формулу: r = g : Q х 100 %, де Q - це максимальна вологість повітря за даної температури.

Розв’яжемо задачу. Визначте відносну вологість повітря, якщо абсолютна вологість становить 6,3 г/м3, а температура повітря +20 °С.

Розв’язок. Для визначення відносної вологості використаємо формулу: r = g : Q х 100 %.

Показник максимальної вологості при температурі +20 °С візьмемо з діаграми (мал. 101 на стор. 129 підручника). Вона дорівнює: Q = 17,3 г/м3. Знайдемо, якою буде відносна вологість: 6,3 г/м3 : 17,3 г/м3 х 100 % = 37 %.

скачать dle 11.0фильмы бесплатно